A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the definite integral by computing an area. -
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Determine the limit algebraically, if possible. -
A) 6
B) 1
C) Does not exist
D) 0
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use the given graph to determine the limit, if it exists.
-
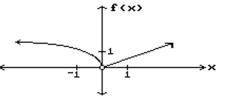
A) Does not exist
B) 0
C)
D) 1
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the problem. -An arrow is shot straight up from level ground. The distance (in meters) of the arrow above the ground (the position function) is at any time (in sec) . Find and the initial velocity of the arrow.
A) ; initial velocity
B) ; initial velocity
C) ; initial velocity
D) ; initial velocity
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the derivative of the function using the definition of derivative. -
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the limit of the function algebraically. -
A)
B)
C) Does not exist
D) 1
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the limit. -Let and . Find .
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use NDER on a calculator to find the numerical derivative of the function at the specified point. - at
A) -1.0000
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the derivative of the function at the specified point. - at
A) 0
B) 9
C) 7
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the indicated limit, if it exists. -
A) 0
B) The limit does not exist.
C) 9
D) 4
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the limit of the function by using direct substitution. -
A) Does not exist
B)
C) 5
D) 0
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the derivative of the function using the definition of derivative. -
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
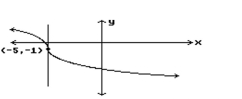
Estimate the slope of the tangent line at the indicated point.
-
A) 0
B) Undefined
C)
D) 1
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the limit of the function algebraically. -
A) Does not exist
B)
C) 0
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the indicated limit. -
A)
B) 0
C) The limit does not exist.
D) 1
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the limit. -Let . Find .
A) 15
B)
C) 6
D) 225
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use a graph of the function to find the derivative of the function at the given point, if it exists. -
A) 0
B) 1
C) Does not exist
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Determine the limit algebraically, if possible. -
A)
B) 1
C) Does not exist
D) 0
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the indicated limit, if it exists. -
A) The limit does not exist.
B) 8
C) 2
D)
Correct Answer

verified
Correct Answer
verified
Showing 21 - 40 of 167
Related Exams